Am I really going to do this? Am I going to spend time on a topic so far from legitimacy as Flat Earth? Doing so risks affording a tiny bit of credibility to an idea that hasn’t earned it, as if I doth protest too much.
Reasons to bother: 1) illustrate direct observation in action; 2) emphasize the power of listening to what the universe tells us rather than insisting on insufficient mental models as “truth”; 3) provide examples of how mental models go wrong; and 4) I made some graphics worth sharing. While a bit of a tangent from my usual “serious” topics, I figure I can have a little fun once in a while.
The focus will be on conspicuous observations anyone can confirm, personally, without too much effort—even from memory, in fact. I’ll skip the literally dozens of ways I have personally measured and confirmed the spherical Earth, which would make for boring reading. Lots of things break in Flat-Earth scenarios, including GPS navigation (no satellites; broken math), gravity (would crumple a disk-Earth into a sphere in no time; plumb bobs would point more north the farther south one went), and what we’ll focus on here: sunsets. No more sunsets, folks—and any sunsets (or sunrises) you might believe yourself to have seen aren’t what you made them out to be, according to Flat-Earthers.
Rather than denigrating the people who subscribe to Flat-Earth beliefs, I’ll focus on observation. I’m not aiming to convince Flat-Earthers; nothing I say (as an obvious shill for the mega-conspiracy) can replace the sense of community and unconditional support they receive from their FE-family. Any of us might go to extremes of twisted and easily-refuted logic to preserve what’s most important to us. Modernity fails humans in countless ways—loss of intimate tribe being among them. We can forgive those seeking to recapture what’s been lost.
The Premise
It’s not possible to lay out the theory of Flat Earth, since there really can’t be one coherent theory consistent with the body of observations, and various factions bicker about various thorny points. But most seem to agree that Earth is a flat disk, wrinkled by terrain, of course. The north pole is at its center, and Antarctica spans the outer periphery like an ice wall circumscribing the disk’s edge. I’m not aware of any Australian versions imposing the polar reverse, which might be construed as yet another slight to the Global South. Actually, the ocean-dominated southern hemisphere is what allows this bias to persist: much harder to “pace off” distances in a car, for instance.
Let’s pause to celebrate the elements of reality here: they agree there are continents and oceans, and that a sort of map can be made, however distorted it may become as one approaches the outer edge. They also acknowledge some special status of the north pole. We can work with this.
As far as I can tell, they also cop to the fact that it’s not noon everywhere at once (time zones are real/necessary), and that some areas on Earth experience nighttime while others are in full daylight. This (reluctant?) admission will turn out to be a serious challenge to their platform, in this post.
Implications: Solar Distance
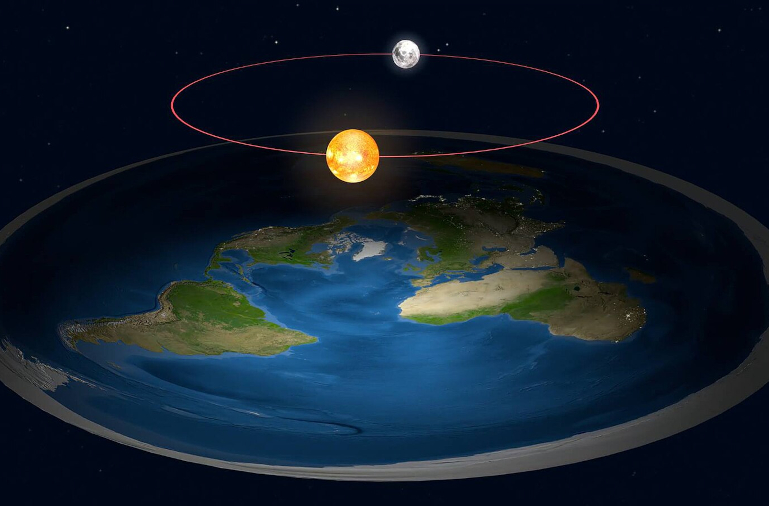
In order to satisfy the previous paragraph, the sun can’t be very far off the disk, and must engage in a sort of spotlighting to concentrate light on one side of the disk while leaving the other in the dark (see banner image).
If the sun were very far (like 25,000 times Earth’s characteristic scale in the round model), its motion would look similar to all Flat-Earth residents: rising and setting at essentially the same time everywhere, simultaneously plunging the whole surface into darkness. No: in a Flat-Earth model the sun must be relatively close to the disk to be seen at different elevations at the same time in different regions of the world, and to account for simultaneous day/night conditions.
Some Flat-Earth enthusiasts build attractive display models that generally include a rotating light extending off a post through the north pole, illuminating one side of the disk at a time. To build a physical model is to have put some thought into where to position the light. Keep going…
Implications: Solar Racetrack
In order to have noon in Los Angeles happen three hours later than noon in New York, the sun has to move over the disk. Because midnight and noon are experienced at the same time on opposite sides of the world (e.g., Venezuela and Borneo), the sun must make some sort of circuit over the disk taking 24 hours to complete a loop, alternating which side it’s on every 12 hours.
Where is this track? Well, it would need to vary seasonally, of course. At the equinoxes, it is easy to experience/confirm the fact that the sun travels directly overhead at all points around what Round-Earthers call the “equator.” In the Flat Earth model, this would be a circle centered around the north pole roughly 10,000 km in radius.
On the solstices, the sun passes overhead all along the Tropics of Cancer and Capricorn: what Round-Earthers call latitudes ±23.5°. No problem, the racetrack circle shrinks to about 7,400 km in June and expands to 12,600 km in December. The math here is that 90 degrees of “latitude” translates to about 10,000 km, and just represents distance from the center of the disk: still an important/real construct.
Solar Height: Satisfying Eratosthenes
Having defined the ground-track path of the sun, the last step is to establish a height for the sun above the disk. Over 2,000 years ago, a dude named Eratosthenes measured Earth’s circumference by using shadow lengths on the same day for positions separated in “latitude.” The simplified idea is that if the sun is directly overhead in some place (only happens in the tropics), the shadow of a vertical pole has zero length, but a pole one degree to the north on a round Earth would be tilted relative to the first by one degree, and would thus sport a shadow whose length is the height of the pole times the tangent of one degree (0.0175). From this observation and measurement of the distance between poles, it is possible to calculate a circumference for Earth—assuming a very distant sun. The technique also works for arbitrary locations, just requiring more trigonometry.
Pole and shadow geometry for a round Earth / distant sun (left) and flat Earth / near sun (right); angles exaggerated for better visibility.
For our Flat Earth: no problem (sort-of): just set the height of the sun off the disk so that a pole one-ninetieth of the 10,000 km pole-to-equator distance north of the first pole casts a one-degree shadow at the same moment. If we denote the equatorial radius as R (~10,000 km), the height becomes 2R/π, or about 6,370 km (awkwardly the round-earth radius, by no coincidence).
Excellent: now we have a fully-defined geometry for solar motion. We’re sciencing!
Implications: No Sunset
We get our first big oops, here. Maybe you saw it coming well in advance, just by glancing at the banner image. In this geometry, the circular track of the sun in the sky satisfies the observations of the overhead-noon-sun in the correct places, and can even account properly for seasonal variations and noon shadow lengths in a band not too far from the sub-sun path. That’s a feat, but there’s more to a day than noon.
Following such a racetrack, the sun never dips below the horizon, or even deigns to get very close. If the sun went below the disk, the entire planet (top-side) would be cast into darkness at once—counter to what we observe so that Flat-Earthers don’t allow this to happen in their mental model.
As seen from the north pole, the equinox sun would ride 32.5° up in the sky all day, rather than the full-circle horizon-skimming motion actually witnessed. At winter solstice, when the north pole endures a months-long dark period, the Flat-Earth sun would still be 27° high in the sky 24/7. Just pretend you don’t see it, or that its light is not beaming toward you, allowing the stars to burst out (the sun’s brightness being suppressed to less than a trillionth its normal radiance, somehow).
At a mid-northern latitude of 35° (like my hometown of Chattanooga), the noon sun would work out reasonably well at summer solstice based on our Eratosthenes-satisfying height, but would be 4° too high at the equinox and 13° too high in December. Far worse, though, is that the midnight sun would be 22° above the northern horizon (29° in summer; 19° in winter). Never a sunset. Oh dear: I’ve seen those!
If the “spotlighting” effect is sufficiently narrow to have the sun go dark at these midnight elevations, then presumably we’d never see the sun when it’s below about 20°. Yet, we do—daily…and brightly.
Fixing Sunset?
Based on the fact that we’ve all seen the sun descend to touch the horizon, what would it take to require the setting sun to get within a quarter-degree of the horizon (half it’s apparent diameter so its bottom edge can touch the horizon, as we know it can)?
Preserving the racetrack path that satisfies 24-hour cycles and high-noon over the appropriate places on Earth, we must lower the sun’s height over the disk to get it low in the sky around the time of sunset. How low? On the equinox track, we would require it to be approximately 50 km up in order for the “setting” sun to get so close to the horizon.
The math, for what it’s worth, is based on where the sun is on the racetrack 6 hours past local noon (at equinox) appearing 1/4° above the horizon from a “latitude” of 35°.
Vrooooom!
We got our sunsets back (sort-of: see silly path graphic below). But at what cost? A sun on a 24-hour schedule around a 10,000-km-radius racetrack moves at 0.73 km/s. If passing overhead 50 km off-the-deck, the zenith angular rate would be about 0.82 degrees per second, which is about 200 times faster than observed—making shadows swing around as if in time-lapse. If overhead at 12:00:00, it would be above 45° elevation angle for only a few minutes: from 11:58:50 to 12:01:10. Don’t bother with the sunscreen. Sun’s got a date in Borneo!
A sun at this height would be above 5 degrees for only 0.2% of Earth’s surface at a time (less than 0.1% for the Flat-Earth disk area, which is larger than the round surface by a factor of pi-over-two-squared: good news for southern real estate!). Anyone farther than 2.5 degrees (280 km) from the sub-sun racetrack latitude would never see the sun more than 10° over the horizon, even in summer. That’s basically the entire U.S. (anything north of 26° latitude). We broke daytime, all so that we could get the sun to flirt with the horizon!
Angular Size
It’s not terribly challenging to confirm that the sun extends approximately half-a-degree on the sky (no matter where in the sky). At our Eratosthenes height of 6,370 km, this would make it about 56 km in diameter. Hey: don’t judge. For our horizon-visiting height, we’re talking 445 meters across to present half-a-degree when straight overhead. Either way, the geometry works out so that if the sun is at constant height over the disk (required for overhead noon observations to all report similar angular size), then when the sun is at 45° above the horizon, it would only appear 70% its customary size, or 0.35° across. At 30° elevation, it’s half the normal size. By the time we let it get down to a quarter-of-a-degree off the horizon, it would be a mere 0.0022° across, or 8 arcseconds (Jupiter and Venus and Saturn are bigger than this in the sky).
Does this sound like the sunsets you’ve enjoyed—a tiny star-like dot just above the horizon, never visibly setting? Didn’t think so.
Graphics
Below is a comparison for two different models of the sun’s apparent trajectory in the sky approaching “sunset” on the equinox, for “latitude” 35 degrees north. The sequence starts three hours after local noon, in 30-minute increments up until 6 hours after noon, when we observe the sun to set, due west. One shows the appearance of a very distant (but correspondingly large) sun in a rotating (round) Earth model, while the other shows the Flat-Earth racetrack at a height satisfying Eratosthenes for the same times. Sizes are exaggerated for all cases by about 3× for better visibility, but notice the small and diminishing size of the Flat-Earth track, and most importantly its refusal to set just before darkness mysteriously kicks in.
These paths are not at all hard to differentiate, even without measurement tools. Now compare to a photo sequence of a sunrise (reflected horizontally to be oriented like my sunset graphic) at a latitude of 43° (Also, it’s worth looking at a gallery of such images).
What sunset looks like for 43° north, bee-lining to the horizon (LynceanEducation; Wikimedia Commons).
Note that the path is a pretty straight line toward the horizon, and that the size is not changing. [I attribute the darker low-elevation instances to a constant exposure time through a dense filter and more atmosphere. The horizon shot removed the filter to get the bright apparition and expose the horizon bathed in sunset colors.]
Most of us have noticed the sun setting due west (or rising due east) around the time of the equinox—especially if driving on streets aligned to the cardinal directions. Many are observant enough to notice the sun rising and setting well to the north of the east–west line in northern-hemisphere summer and well-south of the line in winter. The Flat-Earth sun refuses to comply. In fact, the next plot shows the all-sky view of trajectories and relative sizes at the equinox (again in 30-minute steps; the previous plot is a subset of these exact same positions). One refuses to set, traveling to the north and getting very small (sizes now exaggerated about 10× for better visibility).
All-sky view showing the solar path for three models (round, plus flat at two solar heights).
The FE folks would say the “spotlight” effect makes the sun invisible to us when it’s on the far side of the disk, but one would still never see a sunset, or even the sun close to the horizon! And somehow whatever the sun is doing when far away, its light must be suppressed by at least a factor of a trillion for it to be outshone by the stars. That’s some impressive spotlighting! It’s not sufficient to make an artistic rendering like the banner image. Making the sun effectively invisible while still high in the sky is no joke.
The oddball blob to the south in the polar plot is a “dummy” case of a 50 km-high sun that I contrived to coast “high” in the sky for our test latitude (and made even larger, 15×, to better see the next bit). Looking closely toward the eastern and western horizons, you’ll also see very small—and diminishing—dots trailing toward the north, still at a 30 minute cadence. One would experience a brief flash of daylight lasting less than an hour, then a tiny sun hugging the horizon the rest of the time. Most regions of the planet would not be lucky enough to receive an overhead pass, and would experience a perpetual dim state during which a tiny sun clings to the horizon. That’s no way to live.
Stars
Another easy test: Polaris happens to be very close to the celestial north pole, which means it is basically straight overhead when standing on the north pole (in winter when the sun is—ahem—below the horizon and the sky is dark). It is easy to confirm for those living north of the equator that the angle up to Polaris from the horizon matches your latitude: something I have personally verified across a broad swath of latitudes. At the equator, it’s on the horizon. At “southern” latitudes, it isn’t visible at all, but the undistorted constellation of Ursa Minor and other surrounding asterisms on the northern horizon will point to where it would be, below the horizon, if not straying too far south.
In the Flat-Earth “model,” if stars are “far” then Polaris is straight up no matter where on the disk one goes (easily falsified). If situated lower, it will appear to descend as one travels farther from the pole—as should be the case. But it won’t somehow be on the horizon at the “equator,” and will never creep below the horizon (unless it becomes invisible to all on the flat surface, simultaneously). That would be some news!
Also, if not very, very far away, constellations would become highly distorted as they moved across the sky and toward the horizon, yet we do not witness such behavior and photo-evidence of squeezed constellations is utterly lacking.
Refraction to the Rescue?
Can we somehow fix this mess with refraction? The phenomenon actually goes the other way, making the situation even worse for the Flat-Earth case. Refraction responds to the refractive index of a medium, whose deviation from 1.0000000 (as in vacuum) is proportional to density for a medium like air. Density is proportional to pressure divided by temperature (in absolute scale like Kelvin). Both tend to change with height (climb a mountain and measure for yourself!). We know that the vertical pressure gradient at the surface is always decreasing at approximately −14% per kilometer, while temperature tends to change more modestly (and variably), decreasing by up to −4% (in Kelvin) per kilometer. Because one is in the numerator and the other in the denominator in computing density, these usually cancel somewhat, but pressure always wins. Sometimes a temperature inversion sets up, which serves to amplify the refractive effect on top of what pressure alone does.
The effect is to curve rays down: the opposite of a mirage over hot pavement. Distant objects therefore appear to be higher than they really are. What follows applies to the limiting case of the dry adiabatic lapse rate (steepest temperature profile, in practice), which serves to minimize the effect. Generally, it will be even more pronounced than what I show here. Below is a plot showing raytrace trajectories for light in a density profile decreasing exponentially with height (as observed). The vertical axis is exaggerated by about 300× in order to make out anything at all. Launch angles correspond to 0.25, 0.50, 0.75, 1.0, 1.25, 1.30, 1.33, 1.34, 1.35, and 1.36 degrees above horizontal (the first one is all-but invisible, making it “only” 200 km downrange).
Raytrace trajectories of light refracted by the density gradient in our atmosphere, for a flat geometry (vertically-exaggerated by 300×).
Once above 1.35 degrees, rays “escape” toward infinity. But short of this, sight-lines curve back down toward the Flat Earth. The effect would be the appearance that the ground curves up at its edge, like the lip of a plate! It’s not subtle, either, crawling up to almost three (normal) sun-heights over the horizon! The first degree over the horizon (two sun-heights) catches all terrain within 2,000 km, the rest of the great expanse being progressively squeezed toward a “vanishing line” 1.35 degrees up. Sure: limits to atmospheric transmission would suppress visibility, and intervening air would take on a blue-sky appearance in daytime. But at night! The sparkle of distant cities would become apparent as stationary ground-hugging constellations—the likes of which we’ve never seen, importantly. At midnight, the sunlit side of the planet would shimmer above the northern horizon. Are the Flat-Earther’s even looking for such phenomena? Attenuation is not as serious as it might seem from the distances in the plot, since most of the distant trajectories lie well above the troposphere where attenuation is most pronounced.
Incidentally, the curvature of the low-angle trajectories is about one-sixth that of the round earth (six times the radius), so that the ground falls away far more rapidly than the light curves, resulting in a crisp, local horizon (which is a smidge farther than it would be without refraction).
Hoh boy!
I really could go on and on, as every investigative line opens up a gaping gulf of disconnect between observation and (terribly flawed) “theory.” I suppose a determined Flat-Earther could contrive all sorts of funky effects and twists to bat down one thing at a time (but not in a self-consistent all-hang-together sort of way: just a pile of distracting incoherent “fixes”). Any theory would simultaneously have to nail (to high precision, not just casual glance) the following observations, among many more:
The (solar) experience of a day needs to be the same on a given date for all people at the same “latitude” (distance from north pole) throughout the world.
The non-tiny sun must be able to at least touch the horizon, as we’ve all seen it do.
The angular width of the sun can’t change appreciably (even by 0.02%) across the sky on a given day, aside from a refractive vertical “scrunching” near the horizon.
Likewise, constellations wheel overhead, rising and setting without noticeable distortion, in the same manner for same-latitudes, with north and south poles sharing no stars in common (other than some refracted “bonus” overlap within ~0.5° of the horizon).
A distant flat horizon is crisp rather than curving up and fading: lights from all the cities within thousands of kilometers are not made visible by refraction. The daylight side of the world is not shimmering on the northern horizon.
But can you guess what makes all these myriad observations and more come together without weirdness? Allow Earth to assume a spherical shape—as gravity forces any hunk of rock bigger than a few hundred kilometers to do anyway. We get sunsets back; ships disappear over the horizon rather than curving up while remaining in sight; stars make sense; and constellations don’t scrunch as they get lower in the sky. It’s really a tidy explanation for so much of what we actually witness!
A lesson for me is that these people pay too much attention to their brain chatter and not enough to the actual universe full of sunsets and stars. We could all learn from this: consult the actual universe, not what you would wish to be true. That latter tendency is almost universal: not at all confined to a fringe group. Whether it’s belief that renewable energy will save us, that modernity can in principle continue for thousands of years, or that we’ll colonize space, false beliefs are quite common in our culture. The Flat-Earthers might actually teach us something of immense value, after all.
Note: If you haven’t seen the documentary Behind the Curve, I recommend it—offering a fascinating window into psychology, belonging, and our ability to preserve beliefs in the face of countervailing evidence.
Flat Earth and spotlight sun, by Towarzysz Przewodniczący (Wikimedia Commons)



